【ファイナンス機械学習の勉強メモ】組合せパージング交差検証 (Combinatorial Purged Cross-Validation; CPCV) とは【簡単にわかりやすく】

簡単に解説

CPCV法とは、通常の交差検証では１グループしかテストデータに使わないが、複数グループをテストデータに使い、テストデータの組み合わせを複数得ることによって、バックテスト結果の経路を増やす方法である。

バックテスト経路を複数得ることで、バックテスト結果のシャープレシオも複数得たい、というのがモチベーションだ（シャープレシオ以外のパフォーマンス指標も同様に複数得られる）。通常の交差検証では、バックテスト結果の経路は１つしか得られないので、その経路におけるシャープレシオの値が１つしか得られない。一方で、CPCV法であればバックテスト結果の経路が２つ以上得られるので、バックテスト結果からシャープレシオの分布が手に入る。

交差検証 (Cross-Validation)

CPCV法は通常の交差検証と比較しないと理解できないので、まず交差検証を簡単にレビューする。交差検証とは、未来のデータで訓練したモデルを過去のデータでテストしてもよい、とする方法である。

  • 手元にあるデータは１月から６月のものとする。
  • これを各月のデータに６分割する（１月のデータ、２月のデータ、・・・、６月のデータ）。ファイナンス機械学習ではこの各分割を「グループ」と呼んでいる。
  • 交差検証では、６分割したデータのうち、１グループのみをテストデータに使い、残りの５グループ全てを訓練データに使う。
    • ２月～６月のデータで訓練したモデルを１月のデータでテスト（１月の運用結果を得る）。
    • １月、３月～６月のデータで訓練したモデルを２月のデータでテスト（２月の運用結果を得る）。
    • ・・・
    • １月～５月のデータで訓練したモデルを６月のデータでテスト（６月の運用結果を得る）。
  • これにより、運用結果（バックテスト結果）の経路が１本得られる。すなわち、１月の運用結果、２月の運用結果、・・・、６月の運用結果、という運用結果の経路は１つしか得られない。
    • １月の運用結果は、２月～６月のデータで訓練したモデルを使った場合の１つだけ
    • ２月の運用結果は、１月、３月～６月のデータで訓練したモデルを使った場合の１つだけ
    • ・・・
    • ６月の運用結果は、１月～５月のデータで訓練したモデルを使った場合の１つだけ
  • バックテスト結果の「経路」というのが初めはピンとこないかもしれないが、要するに「バックテスト結果を、テストデータの時系列に並べたもの」である。

CPCV (Combinatorial Purged Cross-Validation)

通常の交差検証ではテストデータ期間を１つずつしか選択しなかったが、CPCV法ではテストデータ期間を複数ずつ選択することで、テストデータ期間の「組み合わせ」を生み出す。交差検証と同じ例で見てみる。

  • 手元にあるデータは１月から６月のものとする。
  • これを各月のデータに６分割する（１月のデータ、２月のデータ、・・・、６月のデータ）。ファイナンス機械学習ではこの各分割を「グループ」と呼んでいる。
  • CPCV法では、６分割したデータのうち、複数グループをテストデータに使い、残りのグループ全てを訓練データに使う。ここでは『ファイナンス機械学習』p212の例にならい、６分割したデータから２つのグループをテストデータに選ぶとする。
    • すると、テストデータの組み合わせは、６から２を選ぶ組み合わせ \({}_6 C_2 = 15\) 通り作れる。 これがp212の図におけるS1からS15である。

以下の図はこちらに公開されている論文から抜粋

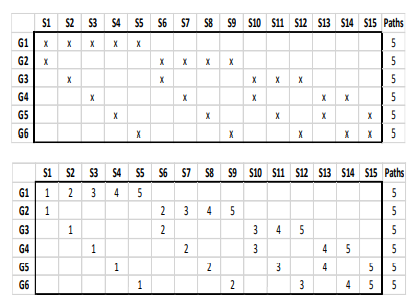
  • xがついているのがテストデータで、空欄が訓練データである。
  • 縦軸のG1からG6が６つのグループ（１月データから６月データ）を表す。
  • ６グループから２グループをテストデータとして選ぶ組み合わせは15通りあり、それが横軸のS1からS15に対応する。
  • S1からS15はそれぞれ、テストデータとして選んだ２グループの組み合わせが異なり、テストデータが異なるということは、テストデータ以外のデータつまり訓練データも異なる。
  • S1からS15はそれぞれ、訓練データとテストデータの内容が異なるので、テストデータから得られる運用結果もそれぞれ異なる。
  • この図から、互いに重複のないバックテスト結果の経路が５通りあることがわかる。
  • 経路の１つ目は、図で「１」となっているグリッドを上から下につないだもの。つまり、
    (G1,S1)→(G2,S1)→(G3,S2)→(G4,S3)→(G5,S4)→(G6,S5)
    である。
    • １月 (G1) のテスト結果は、訓練データに３月～６月 (S1の列で空欄になっている行) を使ったもの
    • ２月 (G2) のテスト結果は、訓練データに３月～６月 (S1の列で空欄になっている行) を使ったもの
    • ３月 (G3) のテスト結果は、訓練データに２月、４月～６月 (S2の列で空欄になっている行) を使ったもの
    • ４月 (G4) のテスト結果は、訓練データに２月～３月、５月～６月 (S3の列で空欄になっている行) を使ったもの
    • ５月 (G5) のテスト結果は、訓練データに２月～４月、６月 (S4の列で空欄になっている行) を使ったもの
    • ６月 (G6) のテスト結果は、訓練データに２月～５月 (S5の列で空欄になっている行) を使ったもの
  • 経路の２つ目は、図で「２」となっているグリッドを上から下につないだもの。つまり、
    (G1,S2)→(G2,S6)→(G3,S6)→(G4,S7)→(G5,S8)→(G6,S9)
    である。
    • １月 (G1) のテスト結果は、訓練データに２月、４月～６月 (S2の列で空欄になっている行) を使ったもの
    • ２月 (G2) のテスト結果は、訓練データに１月、４月～６月 (S6の列で空欄になっている行) を使ったもの
    • ３月 (G3) のテスト結果は、訓練データに１月、４月～６月 (S6の列で空欄になっている行) を使ったもの
    • ４月 (G4) のテスト結果は、訓練データに１月、３月、５月～６月 (S7の列で空欄になっている行) を使ったもの
    • ５月 (G5) のテスト結果は、訓練データに１月、３月～４月、６月 (S8の列で空欄になっている行) を使ったもの
    • ６月 (G6) のテスト結果は、訓練データに１月、３月～５月 (S9の列で空欄になっている行) を使ったもの
  • 全く同様に、３つ目の経路から５つ目の経路も求まる。
  • これらバックテスト結果の５つの経路は、互いに重複していない。
  • 経路１のパフォーマンス指標、経路２のパフォーマンス指標、・・・、経路５のパフォーマンス指標、というように、経路の数だけバックテストのパフォーマンス指標が得られる。
  • 経路の数（いまの場合は５）を示しているのが、『ファイナンス機械学習』p212の \(\phi [N, k] = \frac{k}{N} {}_N C_{N-k}\) である。
  • いまの例だと、\(N = 6, k = 2\) である。つまり、N個のグループがあり、そこからテストデータとしてk個のグループを選んでいる。よって組み合わせの数は、 \({}_N C_{k} = {}_N C_{N-k} = 15\) 通りある。
  • テストデータのグループの総数は、2 x 15 = 30個ある。これが６つのグループに渡って一様に分布しているので、30÷6 = 5通りの経路があることになる。
  • データの分割数を増やすことで、グループ数であるNを増やし、それと同時にテストデータのグループ数であるkをN/2に近づければ、バックテスト結果の経路の数 \(\phi[N, k]\) を大きくすることができる。
  • それによってバックテスト結果のパフォーマンス指標の分布が、細かい粒度で求められる。
  • もちろん、データの分割数を増やすと、訓練データ・テストデータのグループ一つ一つのサイズが小さくなってしまうことに注意。

参考資料

Marcos Lopez de Prado (quantresearch.org)

Cross Validation in Finance: Purging, Embargoing, Combinatorial (quantinsti.com)

あわせて読みたい