【ファイナンス機械学習解説】著者の解説スライドを日本語でまとめてみる (6/10)

シリーズ記事
関連記事
はじめに
参考文献
第６回のスライドに書かれていること
今日学ぶことは何？ (p2)
バックテスト統計量
複数回の検定
複数回検定における第一種の過誤
複数回検定における第二種の過誤
第一種過誤と第二種過誤のトレードオフ
複数回検定におけるPrecisionとRecall
戦略リスクを理解する
参考文献
シリーズ記事
関連記事

シリーズ記事

【ファイナンス機械学習の勉強メモ】組合せパージング交差検証 (Combinatorial Purged Cross-Validation; CPCV) とは【簡単にわかりやすく】 | Quant College

【ファイナンス機械学習の勉強メモ】MDA (Mean Decrease Accuracy) とは | Quant College

【わかりやすく】RANSAC(Random Sample Consensus)とは：アルゴリズム、最小二乗法との違い、読み方 | Quant College

『アセットマネージャーのためのファイナンス機械学習』の詳細目次 | Quant College

はじめに

『ファイナンス機械学習』著者のMarcos Lopez de Prado氏が自身のサイトで『ファイナンス機械学習』に関する講義スライドを全編無料公開している。
『ファイナンス機械学習』については、
botter界隈やシストレ界隈では
・『ファイナンス機械学習』を抱いて寝る人
・『ファイナンス機械学習』を枕にして寝る人
・『ファイナンス機械学習』で枕投げをする人
が続出しているらしく？、
幅広く読まれているようだ。

このシリーズ記事では、著者の了解を得て、上記の講義スライドを日本語でまとめる。英語だとどうしても読むのに時間がかかったりエネルギーを多く使ってしまう、という方向け。全１０回あるが、今回はその第６回のスライドを取り上げる。ログインのような画面になる場合は、メールアドレスとパスワードを入力してSSRNのアカウントを作ればダウンロードできる。

本記事はあくまで当サイト管理人の自習メモである点につきご留意頂きたい。

参考文献

ファイナンス機械学習の続編とも言われている、同じ著者の新しい本はこちら。
(2020/11/12更新)ついに和訳版も出たようだ。

ファイナンス機械学習とその原著はこちら。

第６回のスライドに書かれていること

第６回のスライドでは、バックテスト統計量、複数回検定、戦略リスクなどについて書かれている。

今日学ぶことは何？ (p2)

バックテスト統計量
- 一般的な特徴
- パフォーマンス
- 時間加重リターン
- ドローダウンとTime Under Water
- Implementation Shortfall
- 効率性
複数回検定における第一種の過誤と第二種の過誤
戦略リスクの理解
- 対照的なペイオフ
- 非対称なペイオフ
- 戦略失敗の確率

バックテスト統計量

一般的な統計量 (p4)

タイムレンジ：タイムレンジは開始日と終了日を特定する。
平均AUM：これは運用される資産の平均金額である。
キャパシティー：戦略のキャパシティは、ターゲットとなるリスク調整パフォーマンスを出す最も高いAUMとして計測できる。
レバレッジ：レバレッジは報告されるパフォーマンスを達成するのに必要な借入金額を計測できる。
最大ポジション金額サイズ：最大ポジション金額サイズは、平均AUMを大きく超過する金額のポジションをとるかどうかを示す。
ロングレシオ：ロングレシオは賭けのうちどれくらいの割合をロングポジションに傾けるかを示す。
ベット頻度：ベット頻度は、バックテストにおいて1年あたり何回賭けるかである。
平均保有期間：平均保有期間は平均何日間その賭けをするかである。
年率ターンオーバー：年率ターンオーバーは1年あたりトレードされる金額の平均と、平均年率AUMとの比率を計測する。
原資産との相関：これは戦略のリターンと、それに対応する投資ユニバースのリターンとの相関である。

パフォーマンス (p5)

PnL (P&L、PL、損益) ：バックテストの全期間で生み出されたドルの総額（もしくはドル以外の表示通貨建ての総額）で、最終ポジションの清算コストも含む
ロングポジションのPnL：ロングポジションだけから生み出されたPnL金額の割合
年率リターン：時間加重平均の年率トータルリターンで、配当、利息、コストなどを含む
ヒットレシオ：正のPnLを生んだ賭けの割合
ヒット平均リターン：利益を生んだ賭けから得たリターンの平均
ミス平均リターン：損失を生んだ賭けから得たリターンの平均

時間加重リターン (1/2) (p6)

ポートフォリオ $i$ の区間 $[t-1, t]$ におけるTWRR (Time-Weighted Rate of Return; 時間加重リターン) $r_{i, t}$ は次のように書ける。
$$r_{i, t} = \frac{\pi_{i, t}}{K_{i, t}}$$
$$\pi_{i, t} = \sum_{j=1}^{J}\left[ (\Delta P_{j, t} + A_{j, t})\theta_{i, j, t-1} + \Delta\theta_{i, j, t} (P_{j, t} – \overline{P_{j, t-1}}) \right]$$
$$K_{i, t} = \sum_{j=1}^{J} \widetilde{P_{j, t-1}} \theta_{i, j, t-1} + \max \left\{ 0, \sum_{j=1}^J \overline{\widetilde{P_{j, t}}} \Delta\theta_{i, j, t} \right\}$$
- $\pi_{i, t}$ はポートフォリオ $i$ の時点 $t$ における時価評価 (MtM) 損益
- $K_{i, t}$ はポートフォリオ $i$ で区間 $t$ に渡って運用された資産の市場価値。$\max\left\{ . \right\}$ の項を付けている目的は追加購入（ランプアップ）を考慮するためである。
- $A_{j, t}$ は商品 $j$ 1単位に対して時点 $t$ に発生する金利または支払われる配当。
- $P_{j, t}$ は証券 $j$ の時点 $t$ におけるクリーンプライス。
- $\theta_{i, j, t}$ はポートフォリオ $i$ の時点$t$ における保有残高。

時間加重リターン (2/2) (p7)

続き
- $\widetilde{P_{j, t}}$ は証券 $j$ の時点 $t$ におけるダーティープライス。
- $\overline{P_{j, t}}$ はポートフォリオ $i$ の証券 $j$ の区間 $t$ に渡る平均取引価格（クリーンプライス）。
- $\widetilde{\overline{P_{j, t}}}$ はポートフォリオ $i$ の証券 $j$ の区間 $t$ に渡る平均取引価格（ダーティープライス）。
- 受け取りはその日の初めに起こり、支払いはその日の終わりに起こると仮定する。これら区間ごとのリターンを幾何平均的にリンクしたものを
  $$\phi_{i, T} = \prod_{t=1}^T (1 + r_{i, t})$$
  とおく。
- 変数 $\phi_{i, T}$ はポートフォリオ $i$ に全期間 $t=1, …, T$ に渡って投資された1ドルのパフォーマンスと理解できる。最後に、ポートフォリオ $i$ の年率リターンは
  $$R_i = \left(\phi_{i, T}\right)^{-y_i} – 1$$
  ただし $y_i$ は $r_{i, 1}$ から $r_{i, T}$ までの経過年数である。

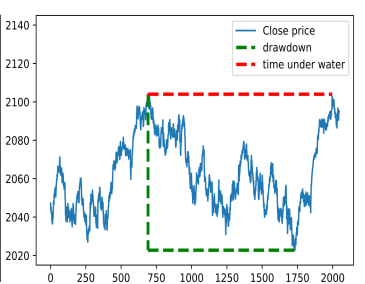
ドローダウンとTime Under Water (p8)

直観的に、ドローダウン (DD) は連続する２つの high-watermarks (HWMs) の間の投資で被った最大損失である。
Time under Water (TuW) はHWMと、PnLがそれまでの最大PnLを超えた瞬間との間で経過した時間である。

Implementation Shortfall (p9)

ターンオーバー当たりのブローカーフィー：これはポートフォリオをターンオーバーするブローカーに支払ったフィー（手数料）であり、取引所フィーを含む。
ターンオーバー当たり平均スリッページ：これはひとつのポートフォリオターンオーバー当たりの、ブローカーフィーを除いた執行コスト。
ターンオーバー当たりドルパフォーマンス：これはドルパフォーマンス（ブローカーフィーとスリッページコストを含む）と、全体ポートフォリオターンオーバーの比率。
執行コスト当たりリターン：これはドルパフォーマンス（ブローカーフィーとスリッページコストを含む）と、執行コスト総額の比率。

効率性 (p10)

年率シャープレシオ：これは、係数 $\sqrt{a}$ で年率に直したシャープレシオ (SR) の値。ここで、$a$ は1年間に観測されたリターンの平均。
インフォメーションレシオ：これは、ポートフォリオに対してSRに相当するもので、ベンチマーク対比でのパフォーマンスを測定する。
確率的シャープレシオ (PSR)：PSRは、正規分布に従わないリターンや、トラックレコードの長さ、によってSRが過大評価される効果を是正するもの。
収縮シャープレシオ (Deflated Sharpe Ratio) (DSR)：DSRは、正規分布に従わないリターン、トラックレコードの長さ、そして複数回テストにおける選択バイアス、によってSRが過大評価される効果を是正するもの。

Sharpe [1966] (p11)

超過リターン（またはリスクプレミア）$\{r_t \}, t = 1, …, T$ がIIDに正規分布に従う投資戦略を考える。
- $r_t \sim N[\mu , \sigma^2 ]$
- ここで $ N[\mu, \sigma^2 ] $ は平均 $\mu $ 分散 $\sigma^2 $ の正規分布を表す。
この戦略の（年率ではない）SRは次で定義される：
- $SR = \frac{\mu}{\sigma}$
パラメーター $\mu, \sigma $ は未知なので、SRは次のように推定される：
- $ \hat{SR} = \frac{\mathbb{E}[\{r_t \}]}{\sqrt{\mathbb{V}[\{r_t \}]}} $

Lo [2002] (p12)

リターンがIIDに正規分布に従うという仮定のもとで、Lo [2002] は $\hat{SR}$ の近似分布を導出した：
- $ (\hat{SR} – SR) \rightarrow N[0, \frac{1}{T} \left(1 + \frac{1}{2} SR^2 \right) ] $
リターンがIIDに正規分布に従わないという仮定のもとで、Mertens [2002] は $\hat{SR}$の近似分布を導出した：
- $ (\hat{SR} – SR) \rightarrow N[0, \frac{1}{T} \left(1 + \frac{1}{2} SR^2 – \gamma_3 SR + \frac{1}{4} \left( \gamma_4 – 3 \right) SR^2 \right) ] $
- ここで、$\gamma_3 $ は $\{r_t \}$ の歪度、$\gamma_4 $ は $\{r_t \}$ の尖度である。（リターンが正規分布に従う場合、$\gamma_3 = 0, \gamma_4 = 3 $ である。）

Bailey and Lopez de Prado [2012] (1/2) (p13)

Christie [2005] と Opdyke [2007] は、実際に、Mertens[2002] の式がより一般的な仮定（必ずしもIIDではなく、リターンが定常でエルゴード性を持つ）のもとでも成り立つことを発見した。
Bailey and Lopez de Prado [2012] はその結果を利用して確率的シャープレシオ（PSR）を導出した。
PSRは観測された $\hat{SR}$ が $SR^* $ を超える確率を次のように推定する：
- $\hat{PSR}[SR^* ] = Z \left[ \frac{(\hat{SR} – SR^* ) \sqrt{T – 1} }{\sqrt{1 – \hat{\gamma_3 }\hat{SR} + \frac{1}{4}(\hat{\gamma_4 } – 1) \hat{SR}^2 }} \right]$
- ここで、$Z[.]$ は標準正規分布のCDF（累積分布関数）、$T$ は観測されたリターンの数、$\hat{\gamma_3} $ はリターンの歪度、$\hat{\gamma_4 }$ はリターンの尖度である。
- $\hat{SR}$ は $SR$ の年率換算前の推定値であり、$T$ 個の観測値と同じ頻度で計算される。

Bailey and Lopez de Prado [2012] (2/2) (p14)

与えられた $SR^* $ に対して、$\hat{PSR}$ は以下の場合に増加する。
- 平均リターン $\mathbb{E}[\{r_t \}]$ が増加したとき
- リターンの分散 $\mathbb{V}[\{r_t \}]$ が低下したとき
- トラックレコード $T$ が長いとき
- リターンが正に歪んでいるとき（$\hat{\gamma_3 }$）
- リターン分布の裾が薄いとき（$\hat{\gamma_4 }$）
この結果によって、次の質問に答えることができる：「推定されたシャープレシオ $\hat{SR}$ が所与の閾値 $SR^* $ を超えることが、統計的有意 ($1-\alpha$) となるのに必要なトラックレコードの長さは？」（最小のトラックレコードの長さ）
- $\mathrm{MinTRL} = 1 + \left[ 1 – \hat{\gamma_3 } \hat{SR} + \frac{1}{4}(\hat{\gamma_4} – 1) \hat{SR}^2 \right] \left( \frac{Z_\alpha }{\hat{SR} – SR^* } \right)^2 $
- ここで、$Z_\alpha $ は右の裾で確率 $\alpha$ を与える標準正規分布のCDFの値である。

Bailey and Lopez de Prado [2014] (1/2) (p15)

収縮シャープレシオ (Deflated Sharpe Ratio; DSR)は、複数回の試行、data dredging, リターンが正規分布に従わないこと、およびサンプルの長さが短いこと、によってシャープレシオ（SR）を過大に見積もる影響をコントロールしたうえで、SRが統計的に有意になる確率を計算する。
$\hat{DSR} = \hat{PSR}(\hat{SR}) = Z \left[\frac{\hat{SR} – \hat{SR_0}\sqrt{T – 1}}{\sqrt{1 – \hat{\gamma_3} \hat{SR} + \frac{1}{4}(\hat{\gamma_4} – 1) \hat{SR}^2 }} \right]$
ここで、$\hat{SR}_0 $ は、False Strategy theoremによって与えられる推定値である。
$\hat{SR}_0 = \sqrt{\mathbb{V}[\hat{SR}_k ]} \left( (1 – \gamma) Z^{-1} \left[ 1 – \frac{1}{K} \right] + \gamma Z^{-1} \left[ 1 – \frac{1}{Ke} \right] \right) $
DSRはSRよりも多くの情報を含んでおり、確率的な形で表現されている。

Bailey and Lopez de Prado [2014] (2/2) (p16)

標準的なSRは２つの推定値の関数として計算される。
- リターンの期待値
- リターンの標準偏差
DSRは５つの追加変数を考慮に入れる（より多くの情報を含んでいる）ことで、SRを低下させる
- リターンの非正規性（$\hat{\gamma_3}, \hat{\gamma_4}$）
- リターン系列の長さ（$T$）
- data dredging の量（$\mathbb{V}[\hat{SR}_k ]$）
- その投資戦略を選択するのに要した独立試行の回数（$K$）
選択バイアスを防ぐうえでカギとなるのは、全ての試行を記録し、実質的に独立な試行の回数（$K$）を正しく定めることである。

複数回の検定

Neymann-Pearsonフレームワーク (p18)

標準的なNeyman-Pearson [1933] 仮説検定フレームワークのもとでは：
- 帰無仮説を $H_0$、対立仮説を $H_1$ と書く
- 検定統計量の分布を、$H_0$ と $H_1$ それぞれのもとで導出する
- 仮に $H_0$ が正しいとした場合に、観測された事象が発生する確率が $\alpha $ しかないとき、$ (1 – \alpha ) $ の信頼水準で $H_0$ を棄却する
このフレームワークは統計学において「背理法」に対応するもの
陽性的中率 (predicted positive) $(x > \tau_\alpha )$ に対応する４つの確率
- $P [x > \tau_\alpha | H_0 ] = \alpha $ は第一種過誤の確率であり、有意水準または偽陽性率という
- $P [x > \tau_\alpha | H_1 ] = 1 – \beta $ は検出力であり、再現率 (recall) または真陽性率という。$P [x \leq \tau_\alpha | H_1 ] = \beta $ は第二種過誤の確率であり、偽陽性率という
- $P [H_0 | x > \tau_\alpha ] $ は False Discovery Rate (FDR) という
- $P [H_1 | x > \tau_\alpha ] $ は検定の適合率/精度 (precision) という
p-値（または $\alpha$）によって帰無仮説 $H_0$ が正しい確率がわかるわけではない

ファミリーワイズエラー率 (FWER) (p19)

Neyman and Pearson [1933] がこのフレームワークを提案した際、検定を複数回行ってベストな結果を選択する、という可能性を考えていなかった
検定を複数回繰り返すと、実質的な $\alpha$ は上昇する
偽陽性の確率が $\alpha$ のとき、検定を２回繰り返したとしよう
- 各試行において、第一種過誤を起こさない確率は $(1 – \alpha )$ である
- もし２回の試行が独立であれば、検定１回目と検定２回目の両方で第一種過誤を起こさない確率は $(1 – \alpha)^2$
- 少なくとも１回、第一種過誤を起こす確率はその残りだから、$1 – (1 – \alpha )^2$
$K$回の独立な検定の後、信頼水準 $(1 – \alpha)^K$ で $H_0$ を棄却する
FWERは、少なくとも１回の陽性が偽である確率、つまり $\alpha_K = 1 – (1 – \alpha)^K$
Sidak Correction：与えられた $K$ と $\alpha_K$ に対して、$\alpha = 1 – (1 – \alpha_K)^\frac{1}{K}$

FWER vs. FDR (p20)

複数回検定の文献における第一種過誤の２つの定義
- ファミリーワイズエラー率 (FWER)：少なくとも１回、偽陽性が発生する確率
- False Discovery Rate (FDR)：偽陽性と陽性的中率の比率の期待値
科学や産業での応用ではたいてい、FWERは過度に懲罰的に考えられている
- 例えば、たった１つの部品に欠陥がある確率をコントロールするような自動車モデルを設計するのは実用的ではないだろう
しかしながら、ファイナンスの文脈では、FDRの使用についてその反対を推奨する
- 理由は、投資家は典型的に、一連の検定における陽性的中率を用いて、全ての戦略に資金を割り当てる、ということはないからである
- そうではなく、投資家は何千、何百万という代替案の中から、ベストな戦略を一つだけ用いる
投資家は、却下された陽性的中率に投資することはできない
- 自動車の例えで言えば、ファイナンスにおいては、モデル一つに対して生産された一つの自動車部品が実際に存在する。生産された部品だけにしか欠陥がなかったとしても、皆がクラッシュするだろう。

複数回検定における第一種の過誤

検定統計量 (p22)

サイズが $T$ のリターン時系列に対して、投資戦略を考える
シャープレシオを推定する：
- $\hat{SR} = \frac{E[\{r_t \}_{t=1,…,T}]}{V[\{r_t \}_{t=1,…,T}]}$
- \{r_t \} は超過リターン
２つの仮説を定義する：
- 帰無仮説 $H_0 : SR = 0$
- 対立仮説 $H_1 : SR > 0$
Bailey and Lopez de Prado [2012] に従い、真のシャープレシオが $SR^* $ とすると、統計量 $\hat{z}[SR^* ]$ は漸近的に標準正規分布に従う
- $\hat{z}[SR^* ] = \frac{ (\hat{SR} – SR^* ) \sqrt{T – 1} }{ \sqrt{1 – \hat{\gamma_3} \hat{SR} + \frac{1}{4}(\hat{\gamma_4} – 1) \hat{SR}^2 } } $
- ただし、$\gamma_3 $ と $\gamma_4 $ はそれぞれ $\{r_t\}$ の歪度と尖度である

Sidak Correction (p23)

複数回検定で第一種過誤が起きる確率は
- $P[\max_k \{\hat{z}[0]_k\}_{k=1,…,K} > z_\alpha | H_0 ] = 1 – (1 – \alpha)^K = \alpha_K $
FWER $\alpha_K $ に対して、Sidak Correctionは単一試行の有意水準を与える：
- $\alpha = 1 – (1 – \alpha_K)^\frac{1}{K}$
すると、帰無仮説が信頼水準 $(1 – \alpha_K )$ で棄却される条件は、
- $ \max_k \{\hat{z}[0]_k \}_{k=1,…,K} > z_\alpha $
- ただし、$z_\alpha = Z^{-1}[1 – \alpha] = Z^{-1}[(1 – \alpha_K )^\frac{1}{K} ]$
- は標準正規分布の右側確率 $\alpha $ の臨界値であり、$Z[.]$ は標準正規分布のCDF

FWERの推定 (p24)

複数回検定における第一種過誤 $\alpha_K $ は以下のように導出できる：

Lopez de Prado and Lewis [2018a] で説明しているクラスタリング手順を試行の相関行列に適用し、クラスターのリターン系列と $E[K]$ を推定する
選択したクラスターのリターンに対して、以下で推定する
- $\hat{z}[0] = \max_k \{\hat{z}[0]_k\}_{k=1,…,K}$
単一試行に対する第一種過誤を求める
- $\alpha = 1 – Z[\hat{z}[0]]$
複数回検定による修正 $\alpha_K = 1 – (1 – \alpha)^K $ を施すと、
- $\alpha_K = 1 – Z[\hat{z}[0]]^{E[K]}$

複数回検定における第二種の過誤

真陽性確率 (p26)

ベストな戦略について対立仮説（$H_1 : SR > 0$）が真であり、$SR = SR^* $ としよう
すると、FWER $\alpha_K $ に対応する検定の検出力は
- $P[\max_k \{\hat{z}[0]_k \}_{k=1,…,K} > z_\alpha | SR = SR^* ]$
- $ = 1 – Z \left[ z_\alpha – \frac{SR^* \sqrt{T – 1} }{ \sqrt{1 – \hat{\gamma_3 } \hat{SR} + \frac{1}{4} ( \hat{\gamma_4 } – 1 ) \hat{SR}^2 } } \right] $
- $ = 1 – \beta $
- ただし、$z_\alpha = Z^{-1} [(1 – \alpha_K )^{1/K} ]$
したがって、検定の検出力は、 $SR^* $、サンプルの長さ、歪度が大きいと上昇する一方で、尖度が大きいと低下する。
検定の検出力は $K$ が大きいと上昇する。なぜなら、複数回検定によって検定の信頼が低下するからである。

$\beta$ の推定 (p27)

複数回検定における第二種過誤 $\beta_K$ は以下のように導出できる

所与のFWER $\alpha_K$ （このFWERは外生的に与えられるか、以前の節で説明した方法で推定される）に対して、単一試行の臨界値 $z_\alpha$ を計算する
シャープレシオが $SR^* $ である戦略が見つからない確率は、$\beta = Z [z_\alpha – \theta ]$ である。ただし、$\theta = \frac{SR^* \sqrt{T – 1}}{\sqrt{1 – \hat{\gamma_3 } \hat{SR} + \frac{1}{4} \hat{SR}^2 } } $

複数回検定における $\beta$ の修正 (p28)

１回の試行において、第二種の過誤を犯す確率が $\beta$ である
$K$ 回の試行において、その全てで第二種の過誤を犯す確率は
- $\beta_K = \beta^K $
FWERとの違いに注意：
- 偽陽性の場合、関心があるのは、少なくとも１回間違う確率である。これはなぜなら、１回でも間違うアラームは失敗だからである。
- しかし、偽陰性の場合、関心があるのは、陽性を全て見逃す確率である

第一種過誤と第二種過誤のトレードオフ

$\alpha_1 $ vs $\beta_1 $ のトレードオフ (p30)

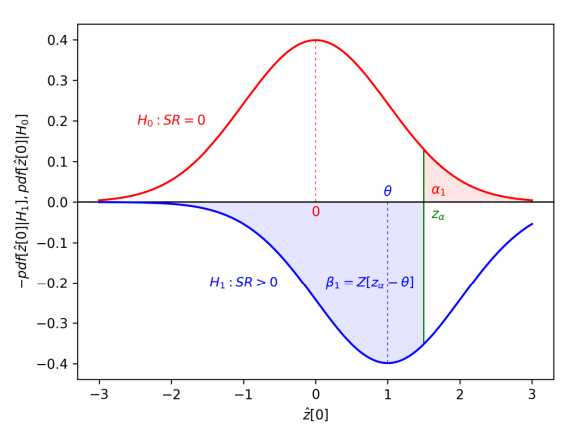
赤色の分布は帰無仮説 $H_0$ が真であるという仮定のもとでの推定量 $\hat{SR}$ の確率をモデル化している
青色の分布（表示の都合上、上下を反転してプロットしている）は、対立仮説 $H_1$ が真であるという仮定、特に、$SR^* = 1$ というシナリオ、のもとでの推定量 $\hat{SR}$ の確率をモデル化している
サンプルの長さ、歪度、尖度はこれら２つの分布の分散に影響を与える
実際の推定値 $\hat{SR}$ が与えられると、これらの変数は確率 $\alpha_1 $ と $\beta_1 $ を定める。片方を低下させると、もう片方が上昇してしまう。

$\alpha_K $ vs $\beta$ のトレードオフ (p31)

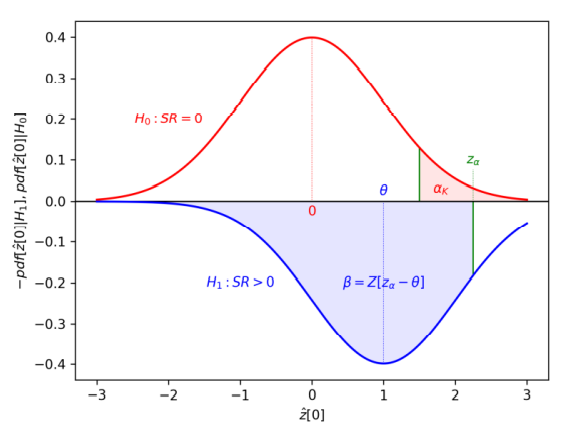
$\beta = Z[Z^{-1} [(1 – \alpha_K )^{1/K}] – \theta ]$
第二種過誤について導出した解析解によって、この $\alpha_K $ と $\beta $ の間のトレードオフが明らかになる。しかし、それは $K=1$ の場合ほど直接的に明らかになるわけではない。
固定された $\alpha_K$ に対して、$K$ が上昇すると、$\alpha$ は低下し、$z_\alpha$ は上昇する。したがって、$\beta$ は上昇する。
しかし、$\beta^K $ はどうなるのか？

$\beta_K$ に与える複合効果は？ (p32)

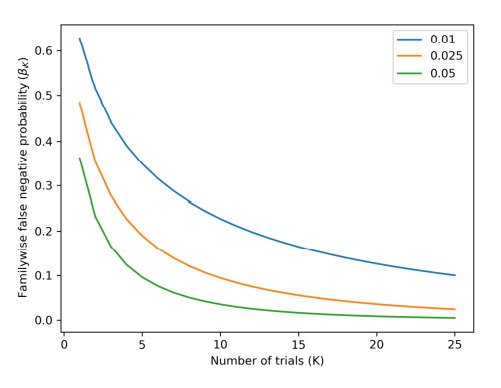
$K$ が上昇すると、２つの互いにぶつかる力が発生する：
１．固定された $\alpha_K $ に対して、$\alpha $ は低下し、$z_\alpha $ は上昇する。したがって、$\beta$ は上昇する。
２．$\beta_K = \beta ^K $ は減少する。
$K$ に対して $\beta$ が上昇するが、全体の効果としては $\beta_K $ は減少する
固定された $\alpha_K$ に対して、$\beta_K $ を $K$ と $\theta$ の関数として定める式は
- $\beta_K = (Z[Z^{-1} [(1 – \alpha_K )^{1/K} ] – \theta ])^K $

複数回検定におけるPrecisionとRecall

単一試行におけるPrecisionとRecall (1/3) (p34)

$s$個の投資戦略を考える。これら戦略の中には偽の発見が含まれるとする。すなわち期待リターンの符号が正ではない戦略が含まれるとする。これらを真の戦略$s_T$個と偽の戦略$s_F$個に分ける。したがって$s=s_T + s_F$である。 $\theta$を、偽の戦略に対する真の戦略のオッズ比としよう。つまり$\theta = \frac{s_T}{s_F}$とおく。金融（計量）経済学のような分野では、シグナル対ノイズの比率が低いので、偽の戦略が多く、したがって、$\theta$は低くなると予想される。真の投資戦略の数は
$$s_T = s\frac{s_T}{s_T + s_F} = s\frac{s_T / s_F}{(s_T + s_F) / s_F} = s \frac{\theta}{1 + \theta}$$
と書ける。
同様に、偽の投資戦略の数は
$$s_F = s – s_T = s \left(1 – \frac{\theta}{1 + \theta}\right) = s \frac{1}{1 + \theta}$$
と書ける。

単一試行におけるPrecisionとRecall (2/3) (p35)

偽陽性率 $\alpha$ （第一種過誤）を所与とすると、偽陽性の数は $FP = \alpha s_F$ となり、真陰性の数は $TN = (1 – \alpha) s_F$ となる。$\alpha$ に対応する偽陰性率（第二種過誤）を $\beta$ とおくと、偽陰性の数は $FN = \beta s_T$ 、真陽性の数は $TP = (1 – \beta) s_T$ となる。したがって検定のprecisionとrecallは、
$$
precision = \frac{TP}{TP + FP} = \frac{(1 – \beta)s_T}{(1 – \beta)s_T + \alpha s_F} = \frac{(1-\beta)s\frac{\theta}{1+\theta}}{(1-\beta)s\frac{\theta}{1+\theta} + \alpha s \frac{1}{1+\theta}} = \frac{(1-\beta)\theta}{(1-\beta)\theta + \alpha}
$$
$$
recall = \frac{TP}{TP + FN} = \frac{(1-\beta)s_T}{(1-\beta)s_T + \beta s_T} = 1-\beta
$$
となる。

単一試行におけるPrecisionとRecall (3/3) (p36)

戦略に対してバックテストを走らせる前に、リサーチャーは戦略が実際に存在するという証拠を集めるべきだ。その理由は、検定のprecisionはオッズ比 $\theta$ の関数だからである。もしオッズ比が低いと、たとえ高い信頼水準（低い p-値）で陽性が得られたとしても、precisionは低いだろう。特に、$(1-\beta)\theta < \alpha$ の場合、戦略は真ではなく偽である可能性が高い。
例えば、バックテストされた戦略でもうかる確率が0.01としよう。つまり、100個の戦略のうち1つが真だから、$\theta = \frac{1}{99}$ である。すると、標準的な閾値である $\alpha = 0.05$ および $\beta = 0.2$ のもとで、リサーチャーは1000回の試行のうち約58回は陽性を得ると期待される。そのうち約8個は真陽性で約50個は偽陽性である。この状況下だとp-値が0.05ということは、偽発見率が86.09%（ざっくり$\frac{50}{58}$）ということになる。この理由だけからも、金融計量経済学における発見のほとんどは偽である可能性が高いと予想すべきである。
この議論により、先ほど達したのと同じ結論が得られる：p-値はあまり参考にならない確率である。統計的検定では、信頼水準が高い（p-値が低い）けれどもprecisionは低い、ということがあり得る。

複数回検定におけるPrecisionとRecall (p37)

既に見たように、少なくとも一回、第一種過誤を犯す確率は
$$\alpha_K = 1 – (1-\alpha)^K$$
である。
一回の試行の後、第二種過誤を犯す確率を $\beta$ とする。$K$回の独立試行の後、それら全てで第二種過誤を犯す確率は $\beta_K = \beta^K$ である。
複数回検定用に調整されたprecisionとrecallは、
$$precision = \frac{(1-\beta_K)\theta}{(1-\beta_K)\theta + \alpha_K} = \frac{(1-\beta^K)\theta}{(1-\beta^K)\theta + 1 – (1-\alpha)^K}$$
$$recall = 1-\beta_K = 1-\beta^K$$
である。

戦略リスクを理解する

対称な損益 (1/2) (p39)

1年にn回の独立同分布の賭けをする戦略を考える。$i \in [1, n]$ 回目の賭けの結果 $X_i$ が、確率 $P[X_i = \pi] = p$ で利益 $\pi$ 、確率 $P[X_i = -\pi] = 1-p$ で損失 $-\pi$ になるとする。
$p$ を二値分類器のprecisionとして見る。ただし陽性は投資機会に賭けることを意味し、陰性は賭けないことを意味する。真陽性では利益を得て、偽陽性では損失を被るが、陰性では（真か偽かを問わず）損益は生じない。
賭けの結果 $\{X_i\}_{i=1,…,n}$ は独立なので、1回の賭けで期待されるモーメント（期待値、分散）は：
- 1回の賭けによる期待利益は $\mathbb{E}[X_i] = \pi p + (-\pi)(1-p) = \pi (2p – 1)$ となる。
- 分散は $\mathbb{V}[X_i] = \mathbb{E}[X_i^2] – \mathbb{E}[X_i]^2$ であり、$\mathbb{E}[X_i^2] = \pi^2 p + (-\pi)^2 (1-p) = \pi^2$ だから、$\mathbb{V}[X_i] = \pi^2 – \pi^2(2p-1)^2 = \pi^2[1-(2p-1)^2] = 4\pi^2 p(1-p)$ となる。
1年にn回の独立同分布の賭けに対して、年率シャープレシオ $\theta$ は
$$\theta[p, n] = \frac{n\mathbb{E}[X_i]}{\sqrt{n\mathbb{V}[X_i]}} = \frac{2p-1}{2\sqrt{p(1-p)}}\sqrt{n}$$
となる。

対称な損益 (2/2) (p40)

上の等式で $\pi$ が（分母分子で）相殺されたことに注意。これは損益が対称だからである。
ガウシアンの場合と全く同様に、$\theta[p, n]$ はスケリーングし直したt-値と理解できる。
このこと（年率シャープレシオに $\sqrt{n}$ がかかっていること）は、たとえ $p > \frac{1}{2}$ が小さくても（50%をわずかにしか超えていなくても）、$n$ が十分大きければシャープレシオは高くなり得る、ということを示している。
これは高頻度取引の経済的基盤であり、$p$ がわずかでも0.5を超えていれば、ビジネス成功のカギは $n$ を増やすことだ。
シャープレシオはaccuracyではなくprecisonの関数である。なぜなら、投資機会に賭けない（陰性）と、直接的には利益も損失も生じないからだ（しかし陰性があまりに多すぎると、$n$ が小さくなり、シャープレシオをゼロに近づけるだろうが）。
- たとえば、$p=0.55$ であれば、$\frac{2p-1}{2\sqrt{p(1-p)}} = 0.1005$ となり、年率シャープレシオ = 2 を達成しようとすると、1年に396回賭けないといけない。

非対称な損益 (p41)

1年にn回の独立同分布の賭けをする戦略を考える。$i \in [1, n]$ 回目の賭けの結果 $X_i$ が、確率 $P[X_i = \pi_+] = p$ で $\pi_+$ 、確率 $P[X_i = -\pi_-] = 1-p$ で $\pi_- < \pi_+$ になるとする。
- 1回の賭けによる期待利益は $\mathbb{E}[X_i] = p\pi_+ + (1-p)\pi_- =(\pi_+ – \pi_-)p + \pi_-$ となる。
- 分散は $\mathbb{V}[X_i] = \mathbb{E}[X_i^2] – \mathbb{E}[X_i^2] $ であり、$\mathbb{E}[X_i^2] = p\pi_{+}^2 + (1-p)\pi_{-}^2 = (\pi_+^2 – \pi_-^2)p + \pi_-^2$ だから、$\mathbb{V}[X_i] = (\pi_+ – \pi_- )^2 p(1-p)$ である。
1年にn回の独立同分布の賭けに対して、年率シャープレシオは
$$\theta[p, n, \pi_- , \pi_+ ] = \frac{n\mathbb{E}[X_i]}{\sqrt{n\mathbb{V}[X_i]}} = \frac{(\pi_+ – \pi_- )p + \pi_-}{(\pi_+ – \pi_- )\sqrt{p(1-p)}}\sqrt{n}$$
であり、$\pi_- = -\pi_+ $ の場合、この等式は対称な場合に帰着することがわかる：
$$\theta[p, n, \pi_- , \pi_+ ] = \frac{2\pi_+ p + \pi_+ }{2\pi_+ \sqrt{p(1-p)}}\sqrt{n} = \frac{2p-1}{2\sqrt{p(1-p)}}\sqrt{n} = \theta[p, n]$$
例えば、$n=260, \pi_- = -0.01, \pi_+ = 0.005, p=0.7$ とすると、$\theta = 1.173$ となる。

戦略が失敗する確率 (1/2) (p42)

上の例の場合、パラメーターについて、
- $\pi_- = -0.01, \pi_+ = 0.005$ はポートフォリオマネージャーが設定し、執行注文によりトレーダーに渡る。
- パラメーター $n=260$ はポートフォリオマネージャーが設定する。どれが賭けに値する機会かを決めるのはポートフォリオマネージャーだからだ。
ポートフォリオマネージャーのコントロール下にない2つのパラメーターは、$p$ （市場によって決定される）と $\theta^* $（投資家によって設定される目標）である。$p$ は未知なので、期待値 $\mathbb{E}[p]$ を持つ確率変数としてモデル化できる。
$p_{\theta^* }$ を下回ると、戦略が目標シャープレシオ $\theta^*$ を下回ってしまう $p$ の値、すなわち $p_{\theta^* } = \max \{p | \theta \leq \theta^* \}$ を定義する。
$p_{\theta^* = 0} = \frac{2}{3}, p < p_{\theta^* = 0} $ の場合、$\theta \leq 0$ となる。このことは、戦略に内在するリスクを浮き彫りにしている。なぜなら，比較的小さな $p$ の低下（$p = 0.7$ から $p = 0.67$ ）であっても、利益が全て消滅してしまうからである。この戦略は、たとえ保有銘柄がリスキーでなかったとしても、本質的にリスクが高い。
これは、ほとんどの資産運用のテキストに欠けている、重要な違いである。戦略リスクはポートフォリオリスクと混同すべきではない。

戦略が失敗する確率 (2/2) (p43)

企業や投資家は、ポートフォリオリスクの計算、監視、報告を行っているが、ポートフォリオリスクが戦略自体のリスクについては何も教えてくれないことに気づいていない。
戦略リスクは、チーフリスクオフィサーが計算するようなポートフォリオのリスクではない。
戦略リスクとは、戦略が時間とともに機能しなくなるリスクであり、チーフインベストメントオフィサーにとって、はるかに大きな意味を持つ問題である。
「この戦略が失敗する確率はどのくらいか」という質問に対する答えは、$\mathbb{P}[p < p_{\theta^*}]$ を計算することに等しい。

参考文献

ファイナンス機械学習の続編とも言われている、同じ著者の新しい本はこちら。
(2020/11/12更新)ついに和訳版も出たようだ。

ファイナンス機械学習とその原著はこちら。

シリーズ記事

【ファイナンス機械学習の勉強メモ】組合せパージング交差検証 (Combinatorial Purged Cross-Validation; CPCV) とは【簡単にわかりやすく】 | Quant College

【ファイナンス機械学習の勉強メモ】MDA (Mean Decrease Accuracy) とは | Quant College

【わかりやすく】RANSAC(Random Sample Consensus)とは：アルゴリズム、最小二乗法との違い、読み方 | Quant College

『アセットマネージャーのためのファイナンス機械学習』の詳細目次 | Quant College

シリーズ記事

関連記事

はじめに

参考文献

第６回のスライドに書かれていること

今日学ぶことは何？ (p2)

バックテスト統計量

一般的な統計量 (p4)

パフォーマンス (p5)

時間加重リターン (1/2) (p6)

時間加重リターン (2/2) (p7)

ドローダウンとTime Under Water (p8)

Implementation Shortfall (p9)

効率性 (p10)

Sharpe [1966] (p11)

Lo [2002] (p12)

Bailey and Lopez de Prado [2012] (1/2) (p13)

Bailey and Lopez de Prado [2012] (2/2) (p14)

Bailey and Lopez de Prado [2014] (1/2) (p15)

Bailey and Lopez de Prado [2014] (2/2) (p16)

複数回の検定

Neymann-Pearsonフレームワーク (p18)

ファミリーワイズエラー率 (FWER) (p19)

FWER vs. FDR (p20)

複数回検定における第一種の過誤

検定統計量 (p22)

Sidak Correction (p23)

FWERの推定 (p24)

複数回検定における第二種の過誤

真陽性確率 (p26)

\(\beta\) の推定 (p27)

複数回検定における \(\beta\) の修正 (p28)

第一種過誤と第二種過誤のトレードオフ

\(\alpha_1 \) vs \(\beta_1 \) のトレードオフ (p30)

\(\alpha_K \) vs \(\beta\) のトレードオフ (p31)

\(\beta_K\) に与える複合効果は？ (p32)

複数回検定におけるPrecisionとRecall

単一試行におけるPrecisionとRecall (1/3) (p34)

単一試行におけるPrecisionとRecall (2/3) (p35)

単一試行におけるPrecisionとRecall (3/3) (p36)

複数回検定におけるPrecisionとRecall (p37)

戦略リスクを理解する

対称な損益 (1/2) (p39)

対称な損益 (2/2) (p40)

非対称な損益 (p41)

戦略が失敗する確率 (1/2) (p42)

戦略が失敗する確率 (2/2) (p43)

参考文献

シリーズ記事

関連記事

タグ一覧

カテゴリー

アーカイブ