目次
関連記事
はじめに
今回は最も簡単な例として、Black-Scholesモデルでバニラオプションを評価してみる。加えて、Greeksを解析解と数値微分の2通りで計算する。その過程で、マーケットデータを切り替えて再評価する手順を学ぶ。掲載するコードは入門者向けにかなり単純化したものなのでその点ご留意頂きたい。
QuantLibでのプライシングの一般的な手順
QuantLibでは様々な商品を多岐に渡るモデル・数値解法でプライシングできるが、その大まかな手順はどれも同じである。すなわち、
(1)商品(Instrument)のオブジェクトを作る
(2)プライシングエンジン(PricingEngine)のオブジェクトを作る
(3)商品にプライシングエンジンをセットする
(Instrumentクラスのメンバ関数 setPricingEngine() を使う)
(4)商品のオブジェクトから .NPV() や .delta() を呼び出す
最終的には、InstrumentとPricingEngineがあればよくて、PricingEngineをInstrumentにSetすることで評価する。Instrumentは取引データから作る。PricingEngineはマーケットデータとモデルデータから作る。
Instrumentを作るには、取引データからPayoffやExerciseなどの部品を作り、その部品を組み合わせてVanillaOptionなどの商品を作る。
PricingEngineを作るには、マーケットデータとモデルデータを組み合わせる。まず、マーケットデータから、原資産価格、イールドカーブ、ボラティリティサーフェイスなどの部品を作る。
次に、モデルデータには、パラメーター、モデルの各種設定、数値計算法の各種設定などがあるが、これらモデルデータと、上記のマーケットデータから作った部品を組み合わせて、確率過程あるいはモデルのオブジェクトを作る。
最後に、確率過程あるいはモデルのオブジェクトと、数値計算法の各種設定を組み合わせて、PricingEngineを作る。
ひとまずInstrumentとPricingEngineの2つを作る、と覚えておこう。
具体例:Black-Scholesモデルでバニラオプションをプライシング
新しいプロジェクトを作りパスを設定
Examplesフォルダ内に新しいプロジェクトを追加し、プロジェクト名をMyBlackScholesとする。
プロジェクトのプロパティからパスを設定する。
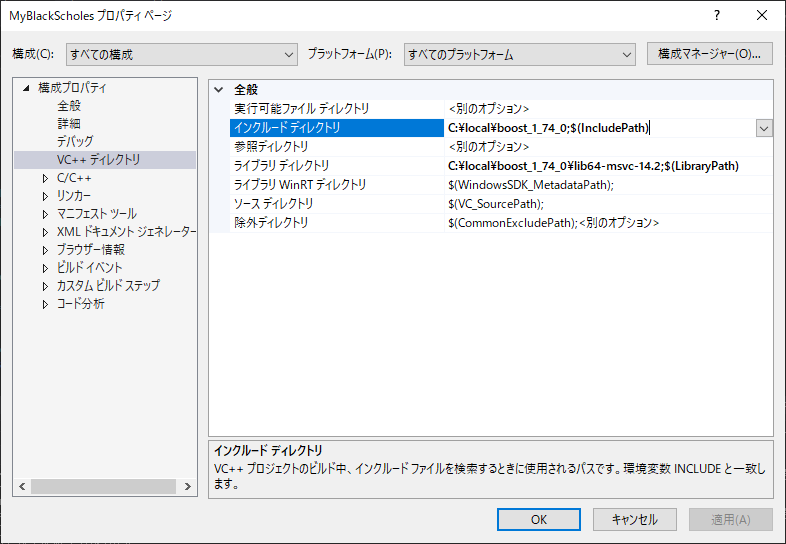
・Boostのヘッダーファイルへのパスを設定
構成プロパティ -> VC++ディレクトリ -> 全般 -> インクルードディレクトリ
に
C:\local\boost_1_74_0
を追加する。このパスは各自で異なるので注意。加えて、このとき、初期設定で入っている $(IncludePath) を上書きして消してしまわないこと。
・Boostのライブラリファイルへのパスを設定
構成プロパティ -> VC++ディレクトリ -> 全般 -> ライブラリディレクトリ
に
C:\local\boost_1_74_0\lib64-msvc-14.2
を追加する。このパスは各自で異なるので注意。加えて、このとき、初期設定で入っている $(LibraryPath) を上書きして消してしまわないこと。
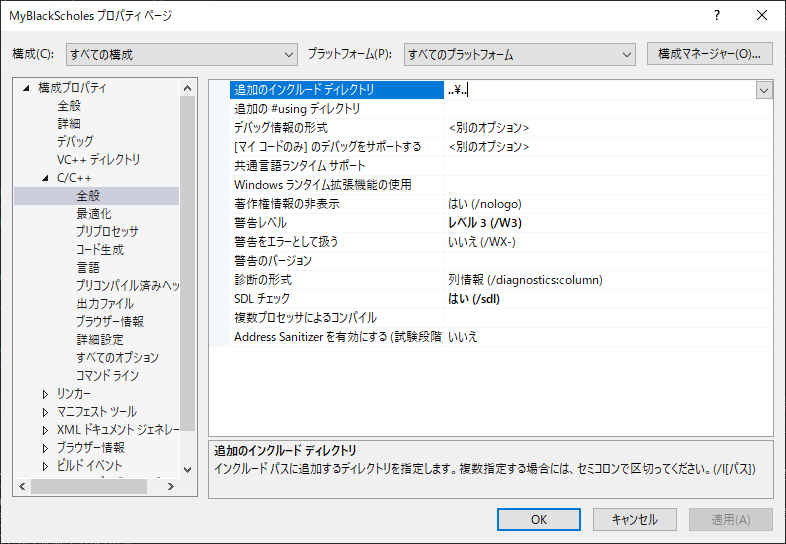
・QuantLibのヘッダーファイルへのパスを設定
以下のように、
構成プロパティ -> C/C++ -> 全般 -> 追加のインクルードディレクトリ
で
..\..
を追加する。
これは2階層上を意味するが、現在のディレクトリ
C:\local\QuantLib-1.19\Examples\MyBlackScholes
から見て、QuantLib-1.19が2階層上だからである。
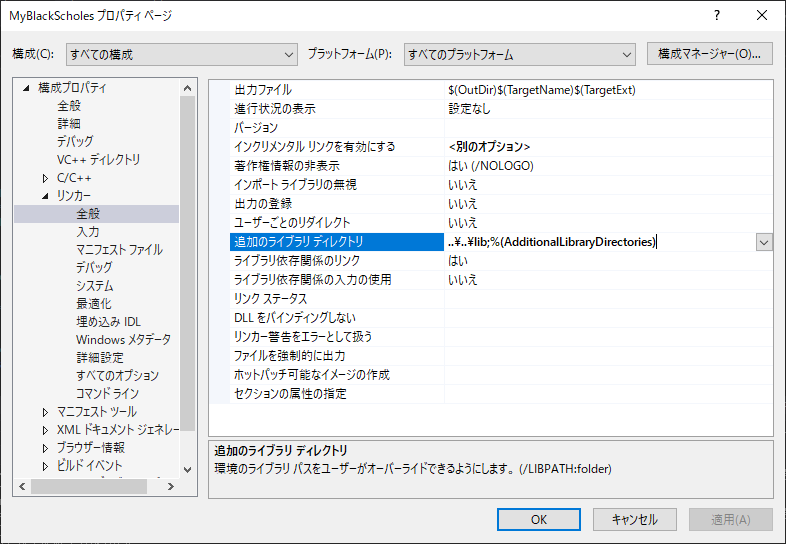
・QuantLibのライブラリファイルへのパスを設定
以下のように、
構成プロパティ -> C/C++ -> 全般 -> 追加のインクルードディレクトリ
で
..\..\lib
を追加する。
これは現在のディレクトリ
C:\local\QuantLib-1.19\Examples\MyBlackScholes
から見て、
C:\local\QuantLib-1.19\lib
を指したい、つまり2階層上のQuantLib-1.19フォルダまで行き、その下のlibフォルダを指したいからである。
ここからは、MyBlackScholesプロジェクト内にソースファイルMyBlackScholes.cppを作り、コードを書いていく。
ソースコード全体
本記事では簡単な例として、次のコードを以下ではセクションごとに説明していく。
#include <ql/quantlib.hpp>
#include <iostream>
using namespace QuantLib;
int main()
{
try {
std::cout << std::endl;
// 日付の設定
Date todaysDate(17, Sep, 2020);
Settings::instance().evaluationDate() = todaysDate;
Calendar calendar = Japan();
DayCounter dayCounter = Actual365Fixed();
// マーケットデータ
Real underlying = 36;
Rate riskFreeRate = 0.01;
Rate dividendYield = 0.00;
Volatility volatility = 0.20;
// 取引データ
Option::Type type(Option::Put);
Date maturity = calendar.advance(todaysDate, 6 * Months);
Real strike = 40;
// 後で数値微分を計算するので値の変化を追跡するためにSimpleQuoteを作る
ext::shared_ptr<SimpleQuote> underlyingQ(new SimpleQuote(underlying));
ext::shared_ptr<SimpleQuote> volatilityQ(new SimpleQuote(volatility));
// マーケットデータのオブジェクトを作る
Handle<Quote> underlyingH(underlyingQ);
Handle<YieldTermStructure> flatRiskFreeTS(
ext::shared_ptr<YieldTermStructure>(
new FlatForward(todaysDate, riskFreeRate, dayCounter)));
Handle<YieldTermStructure> flatDividendTS(
ext::shared_ptr<YieldTermStructure>(
new FlatForward(todaysDate, dividendYield, dayCounter)));
Handle<BlackVolTermStructure> flatVolTS(
ext::shared_ptr<BlackVolTermStructure>(
new BlackConstantVol(todaysDate, calendar, Handle<Quote>(volatilityQ), dayCounter)));
// モデルのオブジェクトを作る
ext::shared_ptr<BlackScholesMertonProcess> bsmProcess(
new BlackScholesMertonProcess(
underlyingH, flatDividendTS, flatRiskFreeTS, flatVolTS));
// PricingEngineを作る
ext::shared_ptr<PricingEngine> bsAnalyticEuropeanEngine(
new AnalyticEuropeanEngine(bsmProcess));
// 取引のオブジェクトを作る
ext::shared_ptr<StrikedTypePayoff> payoff(
new PlainVanillaPayoff(type, strike));
ext::shared_ptr<Exercise> europeanExercise(
new EuropeanExercise(maturity));
VanillaOption europeanOption(payoff, europeanExercise);
// PricingEngineを取引のオブジェクトにセットする
europeanOption.setPricingEngine(bsAnalyticEuropeanEngine);
// NPVとGreeksを解析的に求める
std::cout << "Let us calculate NPV and Greeks by Black-Scholes Analytical Engine:" << std::endl;
std::cout << "NPV = " << europeanOption.NPV() << std::endl;
std::cout << "Delta = " << europeanOption.delta() << std::endl;
std::cout << "Gamma = " << europeanOption.gamma() << std::endl;
std::cout << "Vega = " << europeanOption.vega() << std::endl;
std::cout << std::endl;
std::cout << "Now, let us calculate Numerical Greeks:" << std::endl;
// 数値微分でDeltaとGammaを求める
// 刻みを細かくすると解析解に一致するが、ここではあえて粗くしてみる
const Real dS = 0.1;
Real npv = europeanOption.NPV();
underlyingQ->setValue(underlying + dS);
Real npvPlus = europeanOption.NPV();
underlyingQ->setValue(underlying - dS);
Real npvMinus = europeanOption.NPV();
std::cout << "Numerical Delta = "
<< (npvPlus - npvMinus) / (2. * dS) << std::endl;
std::cout << "Numerical Gamma = "
<< (npvPlus + npvMinus - 2. * npv) / (dS * dS) << std::endl;
// ずらしたインプットを元に戻す
underlyingQ->setValue(underlying);
// 数値微分でVegaを求める
const Real dVol = 0.001;
volatilityQ->setValue(volatility + dVol);
npvPlus = europeanOption.NPV();
volatilityQ->setValue(volatility - dVol);
npvMinus = europeanOption.NPV();
std::cout << "Numerical Vega = "
<< (npvPlus - npvMinus) / (2. * dVol) << std::endl;
// ずらしたインプットを元に戻す
volatilityQ->setValue(volatility);
std::cout << std::endl;
// インプットを元に戻したので元の時価に一致するはず
std::cout << "original NPV = "
<< europeanOption.NPV() << std::endl;
return 0;
}
catch (std::exception& e) {
std::cerr << e.what() << std::endl;
return 1;
}
catch (...) {
std::cerr << "unknown error" << std::endl;
return 1;
}
}出力結果
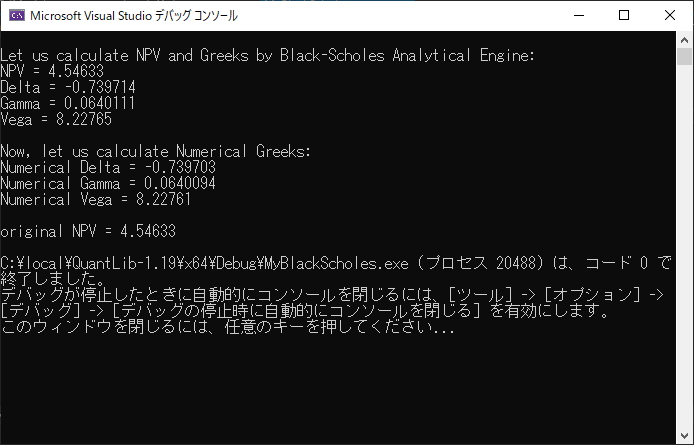
ソースコードの説明
冒頭部分
#include <ql/quantlib.hpp>
#include <iostream>
using namespace QuantLib;初めに必要なヘッダーファイルをインクルードする。
<ql/quantlib.hpp>をインクルードすると、全てのヘッダーがまとめてここにコピペされる。よってこうしておけば、QuantLibの全ての機能を呼び出せるので楽である。しかし、使わない機能もまとめてここにコピペされてしまうため、実行ファイルのサイズが無駄に大きくなる。QuantLibに慣れていれば、自分が必要なヘッダーのみをピックアップしてインクルードするが、この記事は入門者向けなので、簡単のためにまとめて全部インクルードしている。
<iostream>は結果の出力に使う。
usingすることでQuantLibネームスペースに入っているクラスや関数が、頭にQuantLib::と付けることなく利用可能になる。
日付の設定
// 日付の設定
Date todaysDate(17, Sep, 2020);
Settings::instance().evaluationDate() = todaysDate;
Calendar calendar = Japan();
DayCounter dayCounter = Actual365Fixed();欧州をベースに開発されたので、日付は日、月、年、の順で指定。月はEnumになっているので、9月ならSepかSeptemberと指定。
基準日を設定するには、グローバルなSettingsのインスタンスを取ってきて日付をインプットする(SettingsはSingletonパターンで作られている)。
CalendarとDayCounterをどれにするかは実務では重要だが、ここでは適当に設定している。
マーケットデータ
// マーケットデータ
Real underlying = 36;
Rate riskFreeRate = 0.01;
Rate dividendYield = 0.00;
Volatility volatility = 0.20;マーケットデータについて、まずは生の数値をインプットする。
Real、Rate、Volatilityなどについて、実態としてこれらは全てdouble型である。実数を全てdoubleとしてしまうと変数の意味合いが分かりにくいので、typedefで色々な型名が作られている。
今回のコードでは最もシンプルなBlack-Scholesモデルとして、金利、配当利回り、ボラティリティが全てフラットな(期間構造を持たない)場合を考える。
取引データ
// 取引データ
Option::Type type(Option::Put);
Date maturity = calendar.advance(todaysDate, 6 * Months);
Real strike = 40;取引データも同様に、まずは生のデータをインプットしていく。
Call/PutのEnumであるOption::Typeを指定する。
満期はTodayから6Mとする。日付の展開にはCalendarクラスのadvance()メソッドを使う。MonthsはTimeUnitというEnumに含まれるが、*オペレーターがオーバーロードされており、intとTimeUnitを受け取りPeriodを返す。Periodという型は例えば、6M, 1Y, 18M, 2Y, 3Y, …., 30Y, 40Y、といった期間のことを指す。advance()によって、Todayから6か月後の日付を求めている。ここでは3つ目の引数であるBusinessDayConvention、つまり休日調整方法を省略しているが、デフォルトでFollowing(翌営業日に倒す)が設定される。
バニラオプションのストライクを設定する。
マーケットクォートの生成
// 後で数値微分を計算するので値の変化を追跡するためにSimpleQuoteを作る
ext::shared_ptr<SimpleQuote> underlyingQ(new SimpleQuote(underlying));
ext::shared_ptr<SimpleQuote> volatilityQ(new SimpleQuote(volatility));原資産価格とそのボラティリティについては、後ほどデルタとベガを数値微分で計算するので、SimpleQuoteの形にしておく。数値微分ではインプットをずらして時価を再計算するので、インプットが変わったことをInstrumentに伝える必要がある。SimpleQuoteクラスにはsetValue()というメソッドがあり、これで値を変更すると同時に、インプットが変わったことを伝えることができる。このように値が変わったかモニタリングして変わったら関係者に伝える、という一連の手続きは内部的にはObserver/Observableパターンで実装されている。
ext::shared_ptr<> はシェアードポインターであり、新しいバージョンのC++では標準ライブラリに入っているが、古いバージョンのC++だとBoostから呼び出さないといけない。QuantLibは古いバージョンのC++にも対応するよう作られているので、std::shared_ptr<> と boost::shared_ptr<> のどちらを使うかを自動的に切り替えるようになっている。そのためにQuantLibでは ext というネームスペースを作り、その中で std:: と boost:: を切り替えている。
shared_ptr<> は主にポリモーフィズム(多態性)を使うときに出てくる。関数の引数は一般的な型への shared_ptr で定義しておき、その関数を呼び出すときには状況に応じて、より具体的な型への shared_ptr を渡す、というパターンが多い。ここでは、後ほど Quote という一般的な型への shared_ptr、つまり ext::shared_ptr<Quote> を引数としてとるコンストラクタに、Quote を継承した SimpleQuote という具体的な型への shared_ptr つまり ext::shared_ptr<SimpleQuote> を渡す。
マーケットデータのオブジェクト生成
// マーケットデータのオブジェクトを作る
Handle<Quote> underlyingH(underlyingQ);
Handle<YieldTermStructure> flatRiskFreeTS(
ext::shared_ptr<YieldTermStructure>(
new FlatForward(todaysDate, riskFreeRate, dayCounter)));
Handle<YieldTermStructure> flatDividendTS(
ext::shared_ptr<YieldTermStructure>(
new FlatForward(todaysDate, dividendYield, dayCounter)));
Handle<BlackVolTermStructure> flatVolTS(
ext::shared_ptr<BlackVolTermStructure>(
new BlackConstantVol(todaysDate, calendar, Handle<Quote>(volatilityQ), dayCounter)));ここでは目的であるBlackScholesMertonProcessのオブジェクトを作るのに必要な部品を作る。マーケットデータについて、生のデータのままではなく、BlackScholesMertonProcessクラスのコンストラクタに入れられる形に変換しないといけないからだ。
全ての部品に共通するのはHandle<>でくるまれているという点だ。これはBlackScholesMertonProcessに限らず、QuantLibではマーケットデータはHandle<>でくるんだ形でコンストラクタの引数が定義されていることが多い。
ではHandleとは何なのか。これはshared_ptrのshared_ptrである。すなわちshared_ptrを指し示すshared_ptrであり、ポインタのポインタ(ダブルポインタ)のshared_ptrバージョンだと思っておけばよい。実際、Handleのコンストラクタにはshared_ptrを与える。
なぜHandleが必要なのか。それは複数のデータソースの間でインプットを効率良く切り替えるためである。QuantLibではポリモーフィズムをそこら中で使っているため、データはたいていshared_ptrの形になっている。複数のshared_ptrがある中で、使用するデータをあるshared_ptrから別のshared_ptrに切り替えるので、shared_ptrを指し示すshared_ptrが出てくる。あまり正確な説明ではないが初めのうちは上記のようなイメージで押さえておけばいいだろう。
金利と配当利回りはHandle<YieldTermStructure>の形で与える。YieldTermStructureはイールドカーブの期間構造を表す抽象的な型であり、この中で補間が行われる。ここではBSモデルなので期間構造を持たない形でインプットを与える。補間はFlatForwardで行う。
ボラティリティはHandle<BlackVolTermStructure>の形で与える。BlackVolTermStructureはボラティリティサーフェイスを表す抽象的な型であり、この中で補間が行われる。ここではBSモデルなのでボラティリティはフラットであり、BlackConstantVolの形で与える。
いずれもHandleでくるまれており、Handleのコンストラクタにインプットがshared_ptrの形で与えられている。
モデルのオブジェクト生成
// モデルのオブジェクトを作る
ext::shared_ptr<BlackScholesMertonProcess> bsmProcess(
new BlackScholesMertonProcess(
underlyingH, flatDividendTS, flatRiskFreeTS, flatVolTS));作った部品を BlackScholesMertonProcess のコンストラクタに与える。あとはこれを PricingEngine のコンストラクタに与えればいいことになる。
BlackScholesMertonProcess 自体も shared_ptr でくるまれているのは、AnalyticEuropeanEngineのコンストラクタがそう定義されているからだが、実際にはコンストラクタの引数は ext::shared_ptr<GeneralizedBlackScholesProcess> の形で定義されている。GeneralizedBlackScholesProcess は文字通り一般的なBS過程を指しているが、実際にはLocal Volatilityなどかなり幅広い形に対応している。これを継承した型へのshared_ptrであれば何でも受け入れられる。このようにポリモーフィズムを使いたいからshared_ptrでくるまれている。
プライシングエンジンのオブジェクト生成
// PricingEngineを作る
ext::shared_ptr<PricingEngine> bsAnalyticEuropeanEngine(
new AnalyticEuropeanEngine(bsmProcess));作ったモデルオブジェクトをAnalyticEuropeanEngineのコンストラクタに与える。解析解なので数値計算法に関する設定は特に必要なく、引数としてBlackScholesMertonProcessを与えればよい。AnalyticEuropeanEngineはPricingEngineの具体例であり、後ほどInstrumentにSetするにはshared_ptr<PricingEngine>の形にしておく必要がある。
取引のオブジェクト生成
// 取引のオブジェクトを作る
ext::shared_ptr<StrikedTypePayoff> payoff(
new PlainVanillaPayoff(type, strike));
ext::shared_ptr<Exercise> europeanExercise(
new EuropeanExercise(maturity));
VanillaOption europeanOption(payoff, europeanExercise);取引データを組み合わせて取引の部品を作り、それらを使って評価対象の取引オブジェクトを生成する。
ここではVanillaOptionを作るが、引数として必要なのは、shared_ptr<StrikedTypePayoff> と、shared_ptr<Exercise> である。最も簡単な例としてここでは PlainVanillaPayoff と EuropeanExercise をインプットとして与える。
StrikedTypePayoffを継承しているクラスの具体例としては、PlainVanillaPayoff 以外に、AssetOrNothingPayoff, CashOrNothingPayoff, GapPayoff などがある。
Exerciseを継承しているクラスの具体例としては、EuropeanExercise, BermudanExercise, AmericanExercise がある。
プライシングエンジンを取引にセットする
// PricingEngineを取引のオブジェクトにセットする
europeanOption.setPricingEngine(bsAnalyticEuropeanEngine);最後に、取引オブジェクトのsetPricingEngine()でプライシングエンジンをセットする。これでプライシングの準備が完了する。
もしこの後で別のプライシングエンジンを作り、もう一度 setPricingEngine() を呼び出せば、新しいプライシングエンジンでプライシングし直すこともできる。
プライシング
// NPVとGreeksを解析的に求める
std::cout << "Let us calculate NPV and Greeks by Black-Scholes Analytical Engine:" << std::endl;
std::cout << "NPV = " << europeanOption.NPV() << std::endl;
std::cout << "Delta = " << europeanOption.delta() << std::endl;
std::cout << "Gamma = " << europeanOption.gamma() << std::endl;
std::cout << "Vega = " << europeanOption.vega() << std::endl;プライスを出すには取引オブジェクトの .NPV() を呼び出せばよい。Greeksの計算は、.delta(), .gamma(), .vega() などである。プライシングエンジンによってはGreeksの計算に対応していないものもあるので、以下で説明するように数値微分で求めることになる。
数値微分でGreeksの計算
// 数値微分でDeltaとGammaを求める
// 刻みを細かくすると解析解に一致するが、ここではあえて粗くしてみる
const Real dS = 0.1;
Real npv = europeanOption.NPV();
underlyingQ->setValue(underlying + dS);
Real npvPlus = europeanOption.NPV();
underlyingQ->setValue(underlying - dS);
Real npvMinus = europeanOption.NPV();
std::cout << "Numerical Delta = "
<< (npvPlus - npvMinus) / (2. * dS) << std::endl;
std::cout << "Numerical Gamma = "
<< (npvPlus + npvMinus - 2. * npv) / (dS * dS) << std::endl;
// ずらしたインプットを元に戻す
underlyingQ->setValue(underlying);ここでは実験として数値微分でGreeksを計算し、解析解に近い値が出ることを確認する。
重要なこととして、ここでもう一度 .NPV() を呼び出しているが、上で既に .NPV() を呼び出しており、さらにインプットは変化していないため、実際には、この2回目の .NPV() では計算が行われず、格納されている前回の計算結果をそのまま返す。このように、インプットが変化したかどうかをモニタリングするためにObserver/Observableパターンが用いられている。また、インプットが変化した場合に限り再計算が回るようにするために、LazyObjectというデザインパターンが使われている。再計算が必要なときだけ計算を走らせる、というのは特にモンテカルロ法など、計算時間のかかる数値計算法を用いる場合に非常に有効である。
SimpleQuoteクラスの setValue() を呼び出して原資産価格をプラス方向とマイナス方向にずらし、それぞれNPVを再計算する。
ここで重要なのは、原資産価格を変更しても、上でやってきたような、BlackScholesMertonProcessオブジェクトの部品をゼロから作り直す作業は必要ない、ということだ。そのために原資産価格をSimpleQuoteクラスでくるんでおいた、というわけだ。インプットが変化したかどうかをモニタリングできているので、インプットが変化した場合は、.NPV() で再計算が走ってくれる。
インプットをずらした後、元の値に戻すことを忘れずに。
// 数値微分でVegaを求める
const Real dVol = 0.001;
volatilityQ->setValue(volatility + dVol);
npvPlus = europeanOption.NPV();
volatilityQ->setValue(volatility - dVol);
npvMinus = europeanOption.NPV();
std::cout << "Numerical Vega = "
<< (npvPlus - npvMinus) / (2. * dVol) << std::endl;
// ずらしたインプットを元に戻す
volatilityQ->setValue(volatility);ここでは同様にボラティリティをずらしてNPVを再計算することで、Vegaを数値微分で求めている。ボラティリティも原資産価格と同様、SimpleQuoteクラスでくるんでおいたので、setValue() で値を変えても、BlackScholesMertonProcessオブジェクトの部品をゼロから作り直す必要がない。
Greeksの計算結果は、インプットをずらす幅を大きくしたので解析解から少しずれているが、dSやdVolを細かくすると解析解に一致するので、実際に自分で確認してみよう。
おわりに
今回は簡単な例としてBlack-ScholesモデルでVanillaOptionをプライシングする例を紹介した。コードはできるだけ簡略化しているが、それでもshared_ptrや、QuantLibに固有のQuoteやHandleが出てきたので、慣れるまでは難しく感じるかもしれない。ざっくりとしたイメージとして、
・shared_ptrはポリモーフィズム(多態性)を活用するのに使う
・Quoteはインプットの変化をモニタリングするのに使う
・Handleは複数のデータソースを効率的に切り替えるのに使う
というように押さえておけばいったんは大丈夫だと思われる。
今後はより複雑な商品やモデルでのプライシング例を紹介していく予定だが、次回は、Pythonから呼び出すためのラッパーであるQuantLib-Pythonの使い方を紹介したい。